Rekursion

Als rekursive Methoden bezeichnet man Methoden, die sich selbst wieder aufrufen. Ein Haken dabei ist die Tatsache, dass man sich gern das Hirn dabei verrenkt, wenn die Aufrufe allzu kompliziert werden.

Ich versuche ein einfaches Beispiel zu geben. Ich benutze dazu die Klasse Schildkröte, die ihr hier findet.

Für diese Methoden wird ein Applet (oder Application) mit einem Button jButton1 und einem Panel pZeichenbrett benötigt. Das Event ActionPerformed löst dann folgende Methode aus:

private void jButton1ActionPerformed(java.awt.event.ActionEvent evt) {
        Graphics stift = pZeichenbrett.getGraphics();
        Schildkröte fritz = new Schildkröte(400,300,90,stift);   
        zeichneZweiStriche (fritz, 3);
    }

Dazu fehlt natürlich noch die folgende Methode:

    private void zeichneZweiStriche (Schildkröte fritz, int nummer) {
        if (nummer>0) {
            Schildkröte fritz1 = new Schildkröte (fritz.getX(), fritz.getY(), fritz.getWinkel(), fritz.getStift());
            Schildkröte fritz2 = new Schildkröte (fritz.getX(), fritz.getY(), fritz.getWinkel(), fritz.getStift());
            fritz1.dreheLinks(15);
            fritz2.dreheRechts(15);
            fritz1.gehe(20+nummer*20);
            fritz2.gehe(20+nummer*20);
 
            zeichneZweiStriche (fritz1,nummer-1);
            zeichneZweiStriche (fritz2,nummer-1);
        }
    }

Diese Methode bietet nun interessante Variationsmöglichkeiten:

• Die Winkel für die Drehung nach links und rechts können unterschiedlich gemacht werden, um den Baum asymmetrisch zu einer Seite hin zu gewichten.
• Die WInkel können in Abhängigkeit von nummer geändert werden.
• Die Laufweite kann prozentual und zudem noch unterschiedlich geändert werden. Z.B.

  private void zeichneBaum (Schildkröte fabian, int schrittweite, int tiefe) {
          if (tiefe>0) {
              Schildkröte alfred1 = new Schildkröte (fabian.getX(), fabian.getY(), fabian.getWinkel(), fabian.getGraphics());
              Schildkröte alfred2 = new Schildkröte (fabian.getX(), fabian.getY(), fabian.getWinkel(), fabian.getGraphics());
              alfred1.dreheLinks(19);
              alfred2.dreheRechts(15);
              alfred1.gehe(schrittweite);
              alfred2.gehe(schrittweite);
   
              zeichneBaum (alfred1, schrittweite*9/10, tiefe-1);
              zeichneBaum (alfred2, schrittweite*6/10, tiefe-1);
          }
      }

Hier wird der Methodenkopf geändert. Die Laufweite ist als zusätzlicher Parameter eingeführt und muss daher natürlich auch bei sämtlichen Aufrufen mit angegeben werden. Eine Rekursionstiefe größer als 13 macht übrigens wenig Sinn Aufgabe:

1. Schicke Bäume finden
2. dritten Ast hinzufügen

Die Fibonacci-Zahlen sind nichts weiter als eine interessante Folge von Zahlen. Sie werden folgendermaßen definiert:

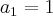
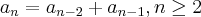
Gesucht ist eine rekursive Methode, die bei Angabe des Parameters n die n-te Fibonacci-Zahl liefert.

Eine Version, die mit Hilfe einer if-Anweisung arbeitet:

    public int fibMitIf(int n) {
        if (n==0) return 0;
        else if (n==1) return 1;
        else return fibMitIf(n-1)+fibMitIf(n-2);        
    }

Eine Version, die ohne die Hilfe einer if-Anweisung aber mit bedingten Ausdrücken arbeitet. (Also doch mit so einer Art if… )

    public int fibOhneIf(int n) {
        return (n==0)? 0 : ((n==1)? 1 : fibOhneIf(n-1) + fibOhneIf(n-2));
    }

Beim Ausdruck Exp1 ? Exp2 : Exp3 wird Exp2 übergeben wenn Exp1 true ist. Ansonsten hat der gesamte Asudruck den Wert Exp3. In der Zeile oben sind zwei dieser bedingten Ausdrücke verschachtelt.

OK, es gibt auch Versionen, die ohne Rekursion arbeiten…

    public int fibOhneRek(int n) {
        int z0=0, z1=1;
        if (n==0) return 0;
        for (int i=1; i<n; i++) {
            int h = z0 + z1;
            z0 = z1;
            z1 = h;
        }
        return z1;
    }

Die Fakultät n! einer natürlichen Zahl n, ist das Produkt sämtlicher natürlicher Zahlen von 1 bis n. (Bsp.: 5! = 5*4*3*2*1)

public int fakultaet (int n) {
    if (n==1)
        return (1);
    else
        return (n*fakultaet(n-1));
}