Ganzkurzauflistung der Themen
- Formale Sprachen und Automaten
- RFC, Internet Message-Format, Alphabet \Epsilon, Wort \Epsilon*, Sprache (Menge der Wörter die was Korrektes ergeben), Grammatik G=(T,N,P,S), Syntaxdiagramm, Produktionen / Regeln P u→v, Ableitung, Worterzeugung, Terminalsymbol T (endet halt), Nichtterminalsymbole N (ist mit Terminalsymbolen weiter definiert), Startsymbol S, Backus-Naur-Schreibweise, JFlap, Ableitungen in Baumdarstellung, EBNF (Wiederholungen, Alternativen) ⇔ BNF ( | für ALternativen), Spracherkennung mit Automaten, Spracherkennungssysteme, Erzeugende Systeme, Analysierende Systeme, endlicher Automat, Akzeptor = erkennender Automat (endl. Zustände Z, Anfangszustand z_a\in Z, Menge von Endzuständen Z_e\subset Z, endl. Eingabezeichen E, Überführungsfunktion \delta:Z\cross E→Z), Sprache Akzeptor, reguläre Ausdrücke ( [] XOR, + Wh min 1, \\Sonderzeichen, () gruppieren, {} genaue Whzahl, ^…$ anfang ende, . beliebiges Zeichen, @ array in Perl), Verknüpfung Wortmengen, Regeln, Spracherkennung mit Parser-Generator, Lexik / Syntax, Gold Parser Builder (Terminalsymbole Ahtml='<'html'> ; Produktionen <HtmlDokument> ::= Ahtml <Kopf> <Rumpf> Ehtml, lexikalische Einheiten, Syntaktische Regeln, Rechenausdrücke, Programmiersprache für Karol, XML,
- Theorie formaler Sprachen, Reguläre Sprachen, Strukturanalyse, Klammersprache K3, rechtslineare Grammatik, Äquivalenzsatz, Sprache → Grammatik → Automat, reguläre Sprache, kontexfreie Sprachen, Kellerautomat - für Klammersprachen, kontextfreie Produktion/Grammatik/Sprache (links-Nichtterminal, rechts beliebig Wort aus Terminalen und Nichtterminalen), kontextsensitive Sprachen, XML, allgemeine/monotone/kontextsensitive Produktionen, MyXML, Turingmaschine, Chomsky-Hierarchie, natürliche Sprachen, Syntax, Semantik, Pragmatik
- Eine Produktion heißt rechtslinear genau dann, wenn auf der linken Seite ein Nichtterminalsymbol steht und die rechts Seite folgende Gestalt hat: (ein Terminalsymbol gefolgt von einem Nichtterminalsymbol) oder (ein Terminalsymbol); alternativ: (ein TErminalsymbol gefolgt von einem Nichtterminalsymbol) oder (das leere Wort). Eine Grammatik heißt rechtslinear / regulär genau dann, wenn alle Produktionen der Grammatik rechtslinear sind. Äquivalenzsatz: Zu jeder rechtslinearen Grammatik gibt es einen nichtdeterministischen endlichen Automaten, der die von der Grammatik erzeugt Sprache erkennt. Zu jedem nichtdeterministischen endlichen Automaten gibt es einen deterministischen endlichen Automaten, der dieselbe Sprache erkennt. Und umgekehrt. Sprache regulär ⇔ durch regulären Ausdruck darstellbar ⇔ von deterministischen endlichen Automaten erkennbar ⇔ nichtdeterministischen endlichen Automaten erkennbar ⇔ von einer rechtslinearen Grammatik erzeugbar
- Semantik von Programmiersprachen, Alphabet (Zeichen), Sprache der Token (Wörter), Sprache der Programme / Tokenfolgen (Sätze), Grammatik, Syntaxanalyse, Scanner (Zeichenfolge → lexikalische Einheiten → Tokenfolge), Scanner-Automat, Parser - Tokenfolge auf syntaktische Korrektheit analysieren, Parserautomat (Kellerautomat), Interpreter - Schritt für Schritt Ausführung, Ausführungstransformation, Transformationsregeln, Übersetzer (QUellsprache → Zielsprache), Übersetzer-Semantik, Übersetzungstransformation
- Automatensimulator, Listen, Stapel, Schlangen, Bäume, Baum-Organisation, Zeiger, OpenXML
- Algorithmen
- Primzahl, Primzahlzwilling, Primzahl nicht neben 6er-Zahl, Programm zur Feststellung von Endlosschleifen, Bedingungsvariable wird in Schleife verändert, selbsthaltend, analyseSelbsthaltend, seltsam (hält, wenn seltsam nicht hält), spezielles Halteproblem: Gibt es ein Programm analyseSelbstanhaltend, das entscheideen kann, ob ein Python-Programm selbsthaltend ist? Eine Sprache über einem Alphabet heißt entscheidbar, wenn es ein Programm gibt, das für jedes Wort über dem Alphabet feststellt, ob es zur Sprache gehört oder nicht. Die Sprache der Python-Quelltexte die zu einem Programm gehören, das bei Eingabe des eigenen Quelltextes hält, ist nicht (Python-)entscheidbar. Termination und Korrektheit sind nicht entscheidbar, Unmöglichkeitsnachweise ⇒ Präzisierung des Algorithmusbegriffs, Algorithmus (endlich, eindeutig, intuitiv: ausführbar, allgemein), ausführbar (maschinenorientiert - Registermaschine, zuordnungsorientiert - E/A-Zuordnungen, anweisungsorientiert - zulässige Anweisungen LOOP/WHILE/PASCAL/DELPHI/JAVA/PYTHON/…), Berechnungsmodell (Problemlösungen selbstständig ausführen, Rechenoperationen ausführen, universell programmierbar, alle Algorithmen ausführen) ⇒ Turingmaschine T={Eingabezeichen X, Bandzeichen B, blank b, Zustände Z, Anfangszustand z0, Überführungsfunktion δ:Z×B → B×{L,R,S}×Z), Zustandgraphen, TuringKara 2 dimensional, f:N→N ist Turingmaschinen-berechenbar: gdw ∃ Turingmaschine T mit endlicher Berechnung von f(x). Turingmaschine soll „Idee“ Computer erfassen (Problemlösungen selbstständig ausführen, Rechenoperationen ausführen, universell, alle Algorithmen), Ziel: ist T wirklich so? universelle Turingmaschine, Turing-Kara, Registermaschine, INC, DEC, JMP, TST, HLT, Registermaschinen-berechenbar, Äquivalenzsatz, anweisungsorient: LOOP - DO - END (terminieren immer), WHILE - DO - END, WHILE-berechenbar ⇔ Registermaschinenberechenbar, Turing-berechenbar ⇔ GOTO-berechenbar ⇔ WHILE-berechenbar, LOOP kann nicht Ackermann, zuordnungsorienterter Ansatz: Präzisierung der E/A-Zuordnungen, Bsp.: primitiv/partiell rekursive Funktionen, f ist primitiv rekursiv ⇔ f lässt sich mit Nachfolgerfunktion s als Grundfunktion, sowie Funktionskomposition und primitiver Rekursion als Konstruktionsoperationen berechnen. das kleinste - Operator, LOOP-berechenbar⇔primitiv rekursiv, WHILE-berechenbar⇔partiell rekursiv, Turing⇔Registermaschinen⇔WHILE⇔partiell rekursiv⇔Pascal - berechenbar, alles führt zur selben Klasse berechenbarer Funktionen: Church-Turing-These: Die Klasse der im intuitiven Sinn berechenbaren Funktinen ist genau die Klasse der Turingmaschinen-berechenbaren Funktionen bzw. die Klasse der partiell rekursiven Funktionen bzw. … Das Berechnungsmodell Turingmaschine / Python programmierbar / … leistet: Es kann Problemlösungen selbstständig ausführen, Rechenoperationen ausführen, ist universell programmierbar, kann alle Algorithmen ausführen. Da das Halteproblem nicht Python-entscheidbar ist, ergibt sich aus der Church-Turing-These, dass das Halteproblem algorithmisch nicht entscheidbar ist.
- Grenzen der Berechenbarkeit - Menge der Turingmaschinen mit bestimmter Zustandszahl ist abzählbar. Menge der Turingmaschinen-berechenbaren Funktionen ist daher auch abzählbar. Existenz nicht-berechenbarer Funktionen (f(n)=fn(n)+1 ⇒ f(n) ∀n∈N), Rado'sche ∑-Funktion, Eine Sprache heißt (Turing-)entscheidbar, wenn es einen Algorithmus (als Turingprogramm) gibt, der für jedes Wort über dem Alphabet feststellt, ob es zur Sprache gehört. Nicht entscheidbar: Halteproblem, Korrektheitsproblem, Wahrheitsproblem, Diophantische Gleichungen. semi-entscheidbar, Gödelsche Unvollständigkeitssätze, Widerspruchsfreiheit, Vollständigkeit, Entscheidbarkeit, Es gibt kein Verfahren, mit dem man für jede beliebige Aussage in endlich vielen Schritten entscheiden kann, ob sie ableitbar ist oder nicht.
- Grenzen der Berechenbarkeit - Patrick Breuer
- Der Komplexitätsbegriff - Aufwandsbestimmung, Additionen zählen, Kursanalyse, 3 Schleifen 1/6n^3+1/2n^2+1/3n, 2 Schleifen 1/2n^2+1/2n, 1 Schleife n
- Beschreibung der Zeitkomplexität - Best, Average, Worst Case, 2^n>n^2>n*log_2(n)>n>log_2(n), Zusammenhang zum Zeitaufwand: 1 Grundoperation pro Millisekunde (1 kHz), Klassifizierung von Algorithmen: Zeitbedarf bei großem Umfang / Zusammenfassen von Komplexitätsklassen die sich nur um einen konstanten Faktor unterscheiden, asymptotische Ordnung O(g(n)) einer Funktion g ist die Menge aller Funktionen f, die für hinreichend große Werte von n nach oben durch ein positives reelles Vielfaches von g beschränkt sind.
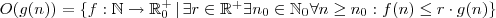
- Abschätzung der Zeitkomplexität - sequentielle / lineare Suche t_{seq}\in O(n), binäre Suche t_{bin}\in O(log_2(n)), Hanoi t_{han}\in O(2^n)
- Praktisch nicht anwendbare Probleme - Ein Algorithmus heßt polynomial (von polynomialer Ordnung), wenn seine Zeitkomplexität durch eine Funktion f(n) beschrieben wird, für die ein k\in N existiert, sodass f\in O(n^k) gilt. Abgeschlossenheit. Ein Algorithmus heißt (praktisch) anwendbar (durchführbar, handhabbar, engl. tractable), wenn er polynomial ist, andernfalls (praktisch nicht anwendbar. Nicht anwendbare Algorithmen werden auch auf zukünftigen Computern nicht anwendbar sein. Die Transformation einer beliebigen Beschreibung eines Algorithmus (Maschinensprache, höhere Programmiersprache, …) in eine äquivalente Turingtafel ist stets mit Polynomialen Aufwand durchführbar. ⇒ Die Definition der Anwendbarkeit von Algorithmen ist maschinenunabhängig. Praxis aknn exponentieller Algorithmus brauchbar sein.
- Praktisch unlösbare Probleme - Ein Problem heßt praktisch lösbar, wenn es einen polynomialen Lösungsalgorithmus für dieses Problem gibt, andernfalls praktisch unkösbar. - Gilt für aktuellen Stand der Forschung, kann noch schneller werden. Königsberger Brückenproblem - Rundweg jede Brücke einmal? Eulerkreis, Nachbar, Grad eines Knoten = Kantenzahl, ungerichteter Graph: ex. Eulerkreis ⇔ alle Knotengrade gerade, Eulerkreis polynomial lösbar, Hamilton-Zyklus Rundweg in einem ungerichteten Graphen der alle Knoten genau einmal enthält. Problem des Handlungsreisenden, Kante mit Kosten, Entscheidungsvariante (ex zu Kosten k eine Rundreise mit Kosten < k?), Zahlvariante (kleinster Kostenwert k, für den eine Rundreise ex.?), Optimierungsvariante (Welches ist die kostengünstigste Rundreise?), Handlungsreisender praktisch unlösbar, Verpackungsproblem (bin-packing-problem): Behälter fester Größe, Gegenstände, Verteilung der Gegenstände auf Behälter, praktisch unlösbar, Stundenplanproblem, Faktorisierung einer n-stelligen natürlichen Zahl, Hanoi
- Nichtdeterministische Algorithmen, P und NP - Hamilton-Zyklus, Darstellung Lösungskandidaten in Auswahlbaum, Backtracking, Acht-Damen-Problem, Pfad erraten und Pfad-Überprüfen sind polynomial lösbar, Praxis: nichtdeterministischer Algorithmus wird durch deterministischen ersetzt / Backtracking, ungünstigster Fall exponentieller Zeitbedarf, dienen der Klassifizierung prinzipiell lösbarer Probleme für die evlt. ein polynomialer Algorithmus existiert, Die Klasse P enthält genau diejenigen Probleme, für die ein polynomialer Lösungsalgorithmus existiert. Die Klasse NP enthält genau diejenigen Probleme, für die folgende Eigenschaften erfüllt sind: ex. Alg. mit exponentiellem Zeitaufwand, Lösung durch nichtdeterministisches Verfahren mit polynomialem Zeitaufwand bestimmbar, ex. polynomialen Verifikationsalgorithmus. P \subset NP \subset prinzipiell lösbare Probleme \subset alle Probleme, NP: Hamilton-Zyklus / Handlungsreisender / Verpackungsproblem / Stundenplanproblem / Faktorisierungsproblem, P=NP?
- NP-Vollständigkeit - Cook: Es ex. die schwersten Probleme in NP. Konjunktiv: deterministischer Algorithmus für ein Problem ⇒ alle Probleme in NP deterministisch polynomial lösbar. Ein Problem heißt NP-vollständig (engl. NP-complete), wenn die folgenden Eigenschaften erfüllt sind: Problem \in NP und Problem \in NP gdw. P=NP. Die NP-vollständigen Probleme sind die schwersten in der Klasse NP. Ein Problem Q_1 heißt polynomial reduzierbar auf ein Problem Q_2, falls es einen polynomialen Algorithmus gibt, der einen Lösungsalgorithmus für Q_2 zu einem Lösungsalgorithmus für Q_1 erweitert: Q_1 \le_p Q_2, Disjunktion (oder) von Variablen oder deren Komplementen heißt Klausel, konjunktive Normalform besteht aus Konjunktionen (und) von Klauseln, boolescher Ausdruck (Variablen durch Operatoren verknüpft) heißt erfüllbar, wenn es eine Belegung der Variablen gibt, sodass der Ausdruck insgesamt wahr wird. Erfüllbarkeitsproblem (engl. satisfiability problem, SAT): Ist ein in konjunktiver Normalform gegebener boolescher Ausdruck B erfüllbar? → NP vollständig! Knotenüberdeckungsproblem (engl. vertex covering problem, VCP): Graph G, k \in N, ex. Teilmenge von G mit k Knoten, sodass jede Kante mindestens einen Endpunkt aus dieser Teilmenge enthält? (Richard Karp, 1972) SAT \le_p VCP, Erbteilungsproblem, k-Färbbarkeitsproblem, Praxisrelevanz: Stundenplan / Handlungsreisender / Reederei Verpackung
- Näherungslösungen - Individuum: Lösungskandidat, Population: Menge von Individuen, Selektion: Auswahl der besten Individuen, Kreuzung: Kombination zweier Individuen zu zwei neuen, Mutation: Zufällige Veränderung eines Individuums, Rucksackproblem, Probabilistischer Algorithmus zum Problem „Independent Set“
- deklarative Programmierung (Logik basiert - Objekte, Eigenschaften, Beziehungen, Konstanten (allg. mit Termen), Prädikate, Fakten, Regeln = Wenn-Dann-Aussagen, Modus Ponens (logische Schlussregel, Variablen sind Platzhalter für alle Objekte der Modellwelt), Wissensbasis, Anfrage, anonyme Variablen, Datenflussrichtung, Berechnungskonzept, Resolution (¬Annahme…) vorwärts entspricht Modus Ponens rückwärts, Backtracking, Beweisbaum, Inferenzmaschine = Unifikationsalgorithmus (erzeugt Variablenbindung) + Inferenzalgorithmus (modus ponens) + Suchalgorithmus (backtracking), Reihenfolge der Prädikate ist relevant! Listen, Konstruktoren ( [], . ), Struktur: .(Element, Liste) → NeueListe, Regel :- , Faktum ohne :- , add3(E,[],[E]). add3(E,[E|X],[E|X]). add3(E,[A|X],[A|M]):-E\==A,add3(E,X,M). del(E,[],E). del(E,[E|X],X). del(E,[A|X],[A|M]):-E\==A,del(E,X,M). gerichtete Graphen, Tiefensuche in zyklenfreien Graphen: weg(X,X). weg(X,Y):-pfeil(X,Z),weg(Z,Y). Wegsuche mit Akkumulator, Breitensuche, deklarative Programmierung besteht darin, den Problemkontext (Miniwelt) mit gegebenen Mitteln (hier:Fakten und Regeln) zu beschreiben. Man beschreibt, welche Eigenschaft das Ergebnis haben soll, das man beim Zusammenfügen erhält. Imperative Programmierung besteht darin, eine (mehr oder weniger abstrakte) Maschine mit Hilfe von Anweisungen zu steuern.
- Vertiefung der objektorientierten Programmierung
Vererbung, Polymorphie, Interfaces
- Vertiefung zur Kommunikation in Rechnernetzen
- Datenaustausch, Zusammenarbeit, Viren, Datenschutz, Morsen, Telegrafie, half-duplex 2 Adern, full-duplex 3 Adern, Transportmedium, serielle Schnittstelle, Nullmodemkabel, Timer, Bitfolgen, Kodierung, meist Zwei Level Kodierung, NRZ-L/M/S, Manchester-Kodierung, DCF77 in BCD ab Bit 21, Timer, Takte, Anfangsbegrenzer AB (Startdelimiter SD), Stoppbit SB, Nutzdaten + Overhead = Rahmen/Frame, selbstsynchronisierend, Zeichen, Puffer, ISO-OSI-Referenzmodell (1 Bitübertragungsschicht - Physical layer, Hub → 2 Sicherungsschicht - Data link layer, Blockbildung Prüfsummen → 3 Netzwerkschicht - network layer, IP → 4 Transportschicht - Transport layer, TCP→ 5 Sitzungsschicht - Session layer → 6 Darstellungsschicht - Presentation layer, Verschlüsselung → 7 Anwendungsschicht - Application layer, E-Mail, Gateway), Trennung Zuständigkeit, Fehler (Änderungen, verloren, Reihenfolge, doppelt, Einzelbitfehler, Doppelbitfehler, Fehlerbündel), Fehler bemerken (Paritätsbits (wieviele Bits sind 1, gerade, ungerade), Prüfsummen (modulo 100), zyklische Redundanzcodes / CRC (Bitfolgen, Polynome, keine Überträge, Daten:Generatorpolynom=Prüfbit, CRC-CCITT=x^16+x^12+x^5+1), Hamming-Code), Quittung, Simplex, Duplex, Quittung oft verloren, Kollisionen, Aloha, slotted Aloha, Carrier Sense Multiple Access Collision Detection CSMA/CD, Kollisionserkennung, -auflösung, Routing, Netzmaske, Netzadresse (erste IP), Broadcastadresse (letzte IP), Wegfindungsproblem, Routingtabelle, Distance-Vector-Algorithmus, Routing Information Protocoll RIP, 1 Hop, Count to infinity, Sniffer,
if ((Absenderadresse XOR Empfängeradresse) AND Netzmaske) == 0) Ziel ist im lokalen Netz else Ziel ist nicht im lokalen Netz
- Socket = jeweilige Ende einer Kommunikationsverbindung, Rechnername, Port-Nr., Client, Server, Streamsocket (Aufbau, Initialisierung, EA, Abbau),
Hier noch eine:
- Graphen
- Graph (Knoten, Kante) = G(V,E) {vertex, edge), Schlingen, (un)gerichtet, (un)bewertet, (un)gerichtet, Erreichbarkeit, Zyklus, Zusammenhang, stark zusammenhängend, Euler-Weg/Euler-Kreis (geschlossenen Weg, der alle Kanten genau einmal besucht), Königsberger Brückenproblem, Haus des Nikolaus, Fahrplan, Navi, Abstände bestimmen, kürzeste Wege bestimmen, Algorithmus von Moore, Algorithmus von Dijkstra, Matrix, Liste, Adjazenz = Nachbarschaft, TGraph, TKnoten, TKante, Verwendung, Eulerbedingung (Zahl der Brücken pro Gebiet bis auf 2 gerade), Zusammenhangsbedingung, Backtracking (Vierfarbenprroblem),
- Grenzen algorithmischer Verfahren; praktische und prinzipielle Grenzen der Berechenbarkeit
- Verifikation der Korrektheit von Algorithmen
Noch eine Auflistung...
- Formale Sprachen - Teil 1 - Beschreibung mit Grammatiken und Erkennung mit Automaten
- Syntaxdiagramm / regulärer Ausdruck / Grammatik /
- Formale Sprachen - Teil 2 - Klassifikation von Sprachen - Exkurs: Semantik von Programmiersprachen
- Kellerautomat / kontextfreie Grammatik / kontextsensitive und allgemeine Sprachen /
- Formale Sprachen - Teil 3
- Scanner / Parser
- Automatensimulator - Entwicklung und Implementierung
- Kommunikation in Rechnernetzen - Teil 1
- Datenübertragung / Modellnetz / Senden und Empfangen von Bitfolgen / programmtechnische Realisierung mit Delphi / Übertragung von Zeichen, Zeichenfolgen, Texten / Übertragungsfehler / Erweiterung zum Bus / Experimente mit Bus
- simplex / half-duplex / full-duplex / Protokoll / Bitrate / Baudrate / Kodierung (No return to Zero - Level, Mark, Space) / (differenzielle) Manchester Kodierung / Synchronisationsvorteil / Startschwierigkeit: Anfangsbegrenzer AB, Startdelemiter SD / Endschwierigkeit: Stop-Bit SB / Bitfolge: Ruhe, AB, Daten, SB, Ruhe / Schichtenarchitekturen: Trennung der Zuständigkeiten, klare Schnittstellen, einfacher Austausche von Schichten, einfaches Zufügen von Schichten / Übertragungsfehler (1 Bit, 2 Bits, n Bits) / Nutzdaten und Prüfbits / Paritätsbit / Summe modulo / CRC (cyclic redundancy check) / Paketverlust / Quittungsbetrieb / geänderte Paketreihenfolge / Duplikate / Send(Stop) and Wait Protokoll / Quittung geht wiederholt verloren / IP-Adressen / Offener Bus / Paket= Ziel+Absender+Daten+CRC / Kollisionen / Aloha: beliebiges Senden, Kollisionen durch Beobachten / slotted ALOHA: beliebiges Senden in quantisierten Zeitabständen / CarrierSenseMultipleAccess-CollissionDetection CSMA-CD / Routing Information Protocol, Distance Vector Algorithmus / Count to Infinity / OSI / Dienste / Protokolle / RFC / (well known) Portnummern / DNS / TCP / Client-Server
- Kommunikation in Rechnernetzen - Teil 2
- Adressen / Kollisionen / Zugriffskontrolle / Routing / RIP / Sniffer
- Logische Programmierung mit Prolog
- Grenzen alogorithmischer Verfahren
- Halteproblem / Berechenbarkeit als Problem / Turingmaschinen und Marienkäfer / Turingmaschine als universelles Berechnungsmodell / Alternative Berechnungsmodelle / Church-Turing-These / Prinzipielle Grenzen der Berechenbarkeit / Blick in die Geschichte
- Praktische Grenzen der Berechenbarkeit (Patrick Breuer)
- Komplexitätsbegriff / Beschreibung der Zeitkomplexität / Abschätzung der Zeitkomplexität an Beispielen / Praktisch nicht anwendbare Algorithmen / Praktisch unlösbare Probleme / Nichtdeterministische Algorithmen, P und NP / NP-Vollständigkeit / Näherungslösungen
- best, average, worst case / Zeitmessungen, Berechnungen / logarithmisch log_2 n, linear n, log-linear n log_2 n, quadratisch n^2, kubisch n^3, exponentiell 2^n / Oh Mann, und noch ganz viel fürchterlicher Kram
- prinzipielle Grenzen der Berechenbarkeit
- Halteproblem / Analyseprogramm / selbsthaltend / seltsam / Entscheidbarkeit / Termination / Korrektheit / (Un-)Möglichkeitsnachweise / intuitiver Algorithmus Begriff: Verarbeitungsvorschrift, die auch für eine Maschine präzise genug ist; eindeutig, ausführbar, endlich, allgemein / … ???
- Objektorientierte Programmierung - Vererbung, Polymorphie
- Graphen - Implementierung, Algorithmen
Falls nicht anders bezeichnet, ist der Inhalt dieses Wikis unter der folgenden Lizenz veröffentlicht: CC Attribution-Noncommercial-Share Alike 4.0 International