Sprachbeschreibung

Noch von vorher…

Kellerautomat: Automat um Kellerspeicher erweitert; kann Kontextfreie Sprachen erkennen
kontextfreie Sprachen: Sprachen, die durch eine kontextfreie Grammatik erzeugt werden
kontextfreie Grammatik: kontextsensitive Grammatik, bei der genau ein Nichtterminal durch Nichtterminale und/oder Terminale ersetzt wird; Bsp: BNF
BNF: Backus-Naur-Form; Metasprache zur Definition kontextfreier Grammatiken; Bsp. aus Wikipedia:

<Programm>               ::= 'PROGRAM' <Bezeichner> 'BEGIN' <Satzfolge> 'END' .
<Bezeichner>             ::= <Buchstabe> <Restbezeichner>
<Restbezeichner>         ::= | <Buchstabe oder Ziffer> <Restbezeichner>
<Buchstabe oder Ziffer>  ::= <Buchstabe> | <Ziffer>
<Buchstabe>              ::= A | B | C | D | ... | Z | a | b | ... | z   *)
<Ziffer>                 ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
<Satzfolge>              ::= ...
...

EBNF: Erweiterte BNF; alles aus EBNF lässt sich auch mit BNF darstellen; EBNF ist nur besser lesbar und kürzer

Grammatiken, Syntaxdiagramme, reguläre Ausdrücke endliche Automaten

Beispiel: Eingabe einer E-Mail-Adresse; Überprüfung auf Korrektheit; Was heießt korrekt?; Aufbau nach RFC 2822 (Requests for Comments - seit 7. April 1969);

Die Menge der korrekt gebildeten E-Mail-Adressen ist eine formale Sprache bestehend aus: Alphabet → Wort → Sprache (Alle gültigen Worte)

Alphabet (stark vereinfacht):

Σ={a, b, c, ., @}

Wort: Hintereinanderreihung endlicher vieler Zeichen aus dem Alphabet.

Σ* ist die Menge aller möglichen Wörter über Σ

(formale) Sprache über Alphabet Σ ist eine Teilmenge von Σ*

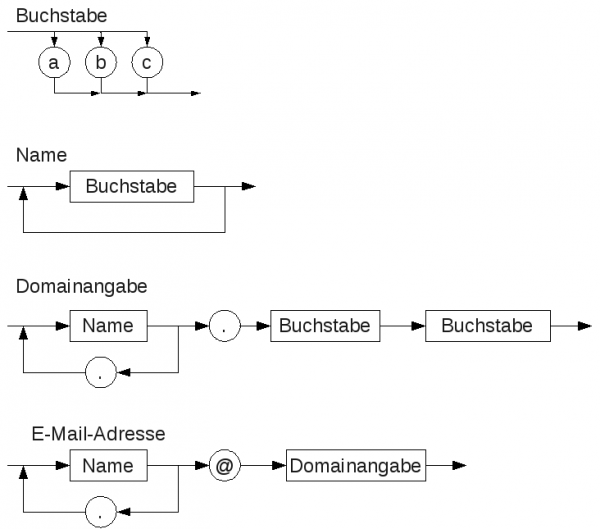
Syntaxdiagramme

Wege durch ein Syntaxdiagramm ergeben

einen Buchstaben
ein Wort
einen korrekten Namen: Name → Buchstabe [→b→] → Buchstabe [→c→] →
eine Domainangabe
eine korrekte E-Mail-Adresse
…

Das Bild als PDF und als ODG zum Bearbeiten.

Nun kann man an Hand der Syntaxdiagramme die Korrektheit von E-Mail-Adressen oder Domainangaben prüfen.

Bestandteile von Syntaxdiagrammen:

Terminalsymbole : Bestandteile des Alphabets zum Aufbau des jeweiligen Konstrukts (z.B. @ und .)
Nichtterminalsymbole: Mit Hilfe weiterer Syntaxdiagramme schon beschriebene Einheiten, die ebenfalls dem Aufbau des Konstruktes dienen. (z.B Name oder Domainangabe)

Übersetzung der Syntaxdiagramme in Produktionsregeln

Die Produktionen (Regeln) zu E-Mail-Adressen mit vereinfachtem Alphabet

Buchstabe	B → a B → b B → c
Name	N → B N → NB
Domainangabe	V → N V → V.N H → BB D → V.H
E-Mail-Adresse	A → N A → A.N E → A@D

Die Ableitung

(auch Worterzeugung) eines Worts durch die Produktionsregeln entspricht einem Weg durch die Syntaxdiagramme. Z.B.:

E -> A@D -> A.N@D -> A.N@V.H -> A.N.N@V.H -> A.N.N@V.N.H -> N.N.N@V.N.H -> N.N.N@N.N.H -> ... -> a.cba.ac@adda.a.ca

Grammatikbegriff

Eine Grammatik besteht aus	Beispiel
einer endlichen nichtleeren Menge T von Terminalsymbolen,	T = {a, b, c, ., @}
einer endlichen nichtleeren Menge N von Nichtterminalsymbolen,	N = {E, D, N, B, A, H, V}
einer endlichen Menge P vpn Produktionen (Regeln) und	P = {B → a, B → b, …, E → A@D}
einem Startsymbol S∈N.	E

Kurz:

G = ( T, N, P, S)

Sprache zur Grammatik

Eine Grammatik G = {T, N, P, S} erzeugt eine Sprache

L(G)

über dem Alphabet T. L(G) ist dabei die Menge der Wörter über T, die vom Startsymbol S mit Hilfe der Produktionen aus P abgeleitet werden können.

Die Backus-Naur-Schreibweise

ist eine Kurzschreibweise für Produktionen. Gibt man eine Grammatik in Backus-Naur-Form an, nutzt man meist die Abkürzung BNF. Beispiel:

Normalform	BNF
B→ a B → b B → c N → B N → BN H → .N H → .NH D → NH E → N@D	B → `a\|b\|c` N → `B \| BN` H → `.N \| .NH` D → `NH` E → `N@D`

Die EBNF

ist eine Erweiterung der BNF. Sie erlaubt einfachere optionale Elemente und Wiederholung von Elementen. Sie kann nicht mehr sondern lediglich einfacher dasselbe darstellen. Beispiel aus Wikipedia:

(* ein einfaches Beispiel in EBNF − Wikipedia *)
Programm = 'PROGRAM' Bezeichner 
           'BEGIN' 
           { Zuweisung [";"] } 
           'END' "." ;
Bezeichner = Buchstabe { ( Buchstabe | Ziffer ) } ;
Zahl = [ "-" ] Ziffer { Ziffer } ;
String = '"' { AlleZeichen − '"'} '"' ;
Zuweisung = Bezeichner ":=" ( Zahl | 
                              Bezeichner |
                              String ) ;
Buchstabe = "A" | "B" | "C" | "D" | "E" | "F" | "G"
          | "H" | "I" | "J" | "K" | "L" | "M" | "N"
          | "O" | "P" | "Q" | "R" | "S" | "T" | "U"
          | "V" | "W" | "X" | "Y" | "Z" ;
Ziffer = "0" | "1" | "2" | "3" | "4" | "5" | "6" 
       | "7" | "8" | "9" ;
AlleZeichen = ? alle sichtbaren Zeichen ? ;