Inhaltsverzeichnis
Schaltungslogik
Logische Gatter
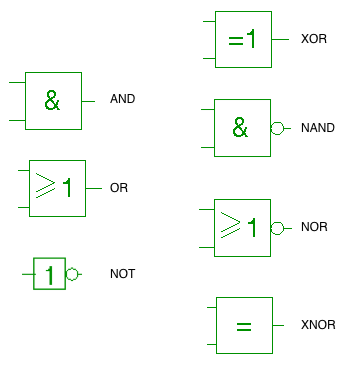
Logische Gatter sind Bauteile, welche die booleschen Verknüpfungen NOT, AND, OR usw. realisieren.Ein solches Gatter ordnet binären Eingangssignalen genau ein binäres Ausgangssignal zu.
- Das Nicht-Gatter (Inverter) realisiert die Negation: $\neg a$ ist genau dann wahr, wenn $a$ falsch ist.
- Das Und-Gatter realisiert die Konjunktion: $a \land b$ ist genau dann wahr, wenn sowohl $a$ als auch $b$ wahr sind.
- Das Oder-Gatter realisiert die Disjunktion: $a \lor b$ ist genau dann wahr, wenn mindestens ein Ausdruck wahr ist.
Das Nicht-Gatter besitzt einen Eingang, die anderen Gatter haben je zwei Eingänge.
Boolesche Terme
- Ein Ausdruck, der aus Variablen und aus Zeichen für Konjunktion, Disjunktion und Negation korrekt gebildet ist, heißt boolescher Term. Jedem booleschen Term entspricht ein binäres Schaltnetz mit einem Ausgang.
- Zwei boolesche Terme sind äquivalent, wenn sie bei jeder Belegung ihrer Variablen mit den Werten 0 und 1 den gleichen Wert haben. Äquivalenten booleschen Termen entsprechen funktionsgleiche Schaltnetze.
- Die Äquivalenz boolescher Terme wird entweder mit Hilfe einer Wahrheitstabelle oder durch Äquivalenzumformungen nachgewiesen.
Übersicht über boolesche Funktionen
Die Gesamtheit aller booleschen Funktionen in zwei Variablen lässt sich in einer Tabelle darstellen.
| a= | 0 | 0 | 1 | 1 | |||
|---|---|---|---|---|---|---|---|
| b= | 0 | 1 | 0 | 1 | Term | Bezeichnung | Sprechweise |
| $f_0$ | 0 | 0 | 0 | 0 | 0 | Nullfunktion | – |
| $f_1$ | 0 | 0 | 0 | 1 | $a\land b$ | Konjunktion | a UND b |
| $f_2$ | 0 | 0 | 1 | 0 | $a \land \neg b$ | Inhibition | a MINUS b |
| $f_3$ | 0 | 0 | 1 | 1 | a | Erste Identität | – |
| $f_4$ | 0 | 1 | 0 | 0 | $\neg a \land b$ | Inhibition | b MINUS a |
| $f_5$ | 0 | 1 | 0 | 1 | b | Zweite Identität | – |
| $f_6$ | 0 | 1 | 1 | 0 | $(\neg a \land b)\lor (a \land \neg b)$ | Antivalenz | a XOR b |
| $f_7$ | 0 | 1 | 1 | 1 | $a \lor b$ | Disjunktion | a ODER b |
| $f_8$ | 1 | 0 | 0 | 0 | $\neg (a\lor b)$ | Negatdisjunktion | a NOR b |
| $f_9$ | 1 | 0 | 0 | 1 | $(\neg a \lor b) \land (a \lor \neg b)$ | Äquivalenz | a ↔ b |
| $f_{10}$ | 1 | 0 | 1 | 0 | $\neg b$ | Zweite Negation | NICHT b |
| $f_{11}$ | 1 | 0 | 1 | 1 | $a\lor \neg b$ | Zweite Implikation | b → a |
| $f_{12}$ | 1 | 1 | 0 | 0 | $\neg a$ | Erste Negation | NICHT a |
| $f_{13}$ | 1 | 1 | 0 | 1 | $\neg a \lor b$ | Erste Implikation | a → b |
| $f_{14}$ | 1 | 1 | 1 | 0 | $\neg (a\land b)$ | Negatkonjunktion | a NAND b |
| $f_{15}$ | 1 | 1 | 1 | 1 | 1 | Einsfunktion | – |
- Die Funktionen $f_0$, $f_3$, $f_5$, $f_{10}$, $f_{12}$ und $f_{15}$ sind nicht von Interesse, da sie eigentlich nullstellige bzw. einstellige Funktionen sind.
- Die Antivalenz heißt auch Exklusiv-Oder oder Addition modulo 2.
Symbole für die logischen Gatter
Rechenregeln der Schaltalgebra
Die mathematische Darstellung einer digitaltechnischen Problemstellung in Form einer schaltalgebraischen Funktionsgleichung ist die kompakteste aller Beschreibungsarten. Zugleich ist sie die Grundlage für eine rechnerische Bearbeitung einer Aufgabenstellung.
Es gelten die folgenden Rechenreglen:
| Bezeichnung der Regel | Rechenregel |
|---|---|
| Bildungsregel | $\neg$ vor $\land$ vor $\lor$ |
| Kommutativgesetz | $a \land b = b \land a$ $a \lor b = b \lor a$ |
| Assoziativgesetz | $a \land (b \land c) = (a \land b)\land c$ $a \lor (b \lor c) = (a \lor b)\lor c$ |
| Distributivgesetz | $a \land (b \lor c) = (a \land b)\lor (a\land c)$ $a \lor (b \land c) = (a \lor b)\land (a\lor c)$ |
| De-Morgan'sche Regeln | $\neg (a \land b) = \neg a \lor \neg b$ $\neg (a \lor b) = \neg a \land \neg b$ |
| Kürzungsregeln | $a \lor (a \land b) = a$ $a \land (a \lor b) = a$ $a \lor (\neg a \land b) = a \lor b$ $a \land (\neg a \lor b) = a \land b$ $(a \land b) \lor (a \land \neg b) = a$ $(a \lor b) \land (a \lor \neg b) = a$ |
Aussagen der Schaltungslogik
Satz 1
Alle zweistelligen booleschen Funktionen können mit Hilfe der Negation, der Konjunktion und der Disjunktion dargestellt werden.
Beweis: Tabelle „Übersicht über boolesche Funktionen“.
Satz 2
Alle zweistelligen booleschen Funktionen können entweder mit Hilfe der Negation und der Konjunktion oder mit Hilfe der Negation und der Disjunktion dargestellt werden.
Beweis: Umformung mit Hilfe der De-Morgan'schen Regeln.
Folgerung: Alle Schaltnetze können mit Redstone-Schaltungen in Minecraft realisiert werden.
Satz 3
Alle zweistelligen booleschen Funktionen können entweder mit Hilfe der NAND-Verknüpfung oder mit Hilfe der NOR-Verknüpfung dargestellt werden.
Beweis: Drücke Negation, Konjunktion und Disjunktion mit Hilfe von NAND- bzw. NOR-Verknüpfungen aus. Beispiel: $\neg x = \neg (x \land x) = x \mbox{ NAND } x$.
Folgerung: Alle Schaltnetze können aus Gattern einer einzigen Art aufgebaut werden.
Disjunktive Normalform und Schaltnetze
Disjunktive Normalform
Ein boolescher Term ist in disjunktiver Normalform, wenn er eine Disjunktion von Kunjunktionstermen ist. Ein Konjunktionsterm wird durch Konjunktion von negierten oder nichtnegierten Variablen gebildet. Beispiel: $(a \land \neg b \land \neg c \land d) \lor (\neg a \land b \land c \land d) \lor (a \land b \land \neg c \land d)$ (Die Klammern dürfen wegen $\neg$ vor $\land$ vor $\lor$ auch weggelassen werden.)
Schaltnetze aus Termen in disjuntiver Normalform
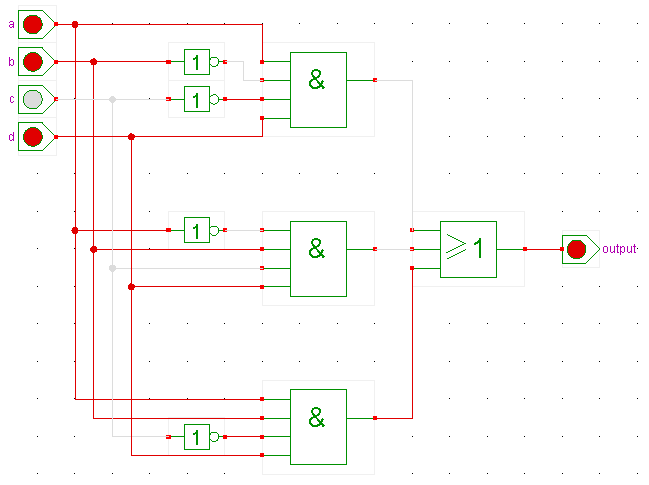
Ein Term in disjunktiver Normalform lässt sich als Schaltnetz einfach verwirklichen. Jeder einzelne Konjunktionsterm wird mit einem Mehrfach-AND realisiert, die Eingänge werden ggf. vorher negiert. Die Ausgänge dieser Mehrfach-AND-Bausteine werden in ein Mehrfach-ODER zusammengeführt. Beispiel:
In der Praxis ist es natürlich sinnvoller, den Term vorher (z.B. mit Kürzungsregeln) zu vereinfachen.
Disjunktive Normalformen aus Wahrheitstabellen
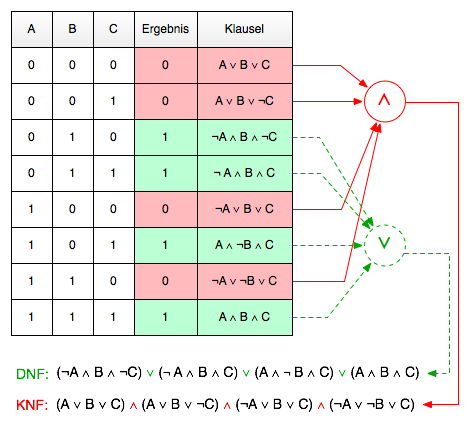
Zur Bildung eines booleschen Terms in disjunktiver Normalform genügt es, die Zeilen der Wahrheitstabelle abzulesen. Für jede Zeile, die als Resultat eine 1 liefert, wird eine Konjunktion gebildet, die alle Variablen verknüpft. Variablen, die in der Zeile mit 1 belegt sind, werden dabei nicht negiert und Variablen, die mit 0 belegt sind, werden negiert. Durch disjunktive Verknüpfung dieser Terme erhält man die disjunktive Normalform.
Die Abbildung aus Wikipedia zeigt die Bildung der disjunktiven Normalform (grün) und der konjunktiven Normalform (rot):
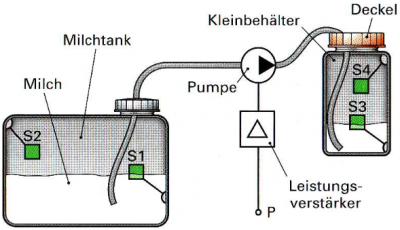
Aufgabe: Pumpensteuerung
Auf einem Bauernhof wird Milch zunächst in einem großen Vorratsbehälter gesammelt und von dort in einen Kleinbehälter gepumpt. Aus diesem Kleinbehälter entnehmen die Kunden im Hofladen die gewünschte Menge Milch.
- Die Pumpe darf nicht leer laufen.
- Der Mindestfüllstand im Kleinbehälter darf nicht unterschritten werden.
- Erstelle eine Wahrheitstabelle für die Steuerung der Pumpe und bilde daraus einen Term in disjunktiver Normalform.
- Zeige, dass der Term äquivalent ist zu $\neg S4 \land S1$.
- Erweitere die Wahrheitstabelle durch ein Steuersignal für einen Alarm, der eine Fehlfunktion anzeigen soll. Erstelle auch hierfür einen booleschen Term.
Aufgabe: 7-Segment-Anzeige
Auf den 4 Eingängen w, x, y, z liegt ein binär codierter Wert zwischen -1 und 16. Die 7-Segment-Anzeige soll diesen als Hexadezimalziffer anzeigen. Überlege dir sinnvolle Layouts für die Zahlen a bis f. Bestimme einen booleschen Term für das mittlere Segment g.
