Sortierverfahren

Dieser Text stammt aus dem Jahre 2001.

Die Problemstellung ist einfach und klar definiert: Gegeben ist ein Array mit Elementen, die nach ihrem Schlüssel sortiert werden können, über deren momentane Anordnung jedoch nichts bekannt ist (das heißt natürlich auch, dass sie theoretisch schon sortiert sein könnten oder genau in der umgekehrten Reihenfolge vorliegen könnten). Der Sortieralgorithmus soll die Elemente in die richtige Reihenfolge bringen. Eine einfache Frage, viele Antworten:

Bubblesort ist einer der simpelsten Sortieralgorithmen. Die Idee dahinter ist die folgende: Im ersten Durchgang wird das Array vom Ende bis zum Anfang durchgegangen und in jedem Schritt das aktuelle Element mit dem nächsten verglichen. Ist das hintere kleiner, werden die beiden vertauscht, so dass größere Elemente am Weg liegenbleiben und das jeweils kleinste weiter nach vorn wandert. Am Anfang angekommen, liegt das kleinste Element des Arrays an Position 1, wo es auch hinsoll. Im nächsten Durchlauf wird dann das zweitkleinste Element gesucht und nach vorne durchgereicht. Logischerweise muss dieser Durchlauf nicht ganz bis zum Anfang gehen, sondern nur bis Index 2. Im dritten Durchlauf braucht nur bis Index 3 gegangen zu werden usw., bis das Verfahren abgeschlossen ist.

Man kann sich vorstellen, dass die kleineren Elemente „leichter“ sind und daher aufsteigen wie Blasen - daher der Name Bubblesort. Ohne weitere Umschweife hier der Algorithmus:

                         const TableSize = 20; //Array-Obergrenze
                         type TableArray: array[1..TableSize] of Byte;
 
                         procedure BubSort(var Table: TableArray);
                         var
                           Run: LongInt;
                           Index: LongInt;
                           x: Byte;
                         begin
                           for Run := 2 to TableSize - 1 do
                             for Index := TableSize downto Run do
                               if Table[Index] < Table[Index - 1] then
                               begin
                                 x := Table[Index];
                                 Table[Index] := Table[Index - 1];
                                 Table[Index - 1] := x;
                               end;
                         end;

Deutlich zu erkennen ist der Vertauschungsvorgang, bei dem das „untere“ Element zunächst in der Variablen x zwischengespeichert wird, dann den Wert des „oberen“ zugewiesen bekommt und anschließend x im „oberen“ Index gespeichert wird. Bubblesort genießt keinen besonders guten Ruf, weil es sehr langsam ist. Trotzdem gehört es zu denjenigen Algorithmen, die man häufiger antrifft, nicht zuletzt wegen seines hohen Bekanntheitsgrades. Hat man nur kleine Arrays zu sortieren (z. B. 20 bis 50 Elemente), schlägt es sich in der Regel auch ganz wacker; für größere Arrays hingegen ist es nicht zu empfehlen. Ich habe mir vorgenommen, auf dieser Seite vollkommen auf Komplexitätsanalysen zu verzichten, wenn es jemanden interessiert - die Literatur quillt über davon

Selectionsort ist ebenfalls ein sehr einfacher Algorithmus. Das Prinzip hinter dem „Sortieren durch Auswählen“ besteht darin, dass das Array von vorn nach hinten durchgegangen wird, und für jeden Platz das passende Element herausgesucht wird.

Als erstes betrachtet man also das Element am Index 1. Man geht dann das Array Element für Element durch und merkt sich, welches das kleinste ist. Dieses vertauscht man dann mit dem ersten, so dass ganz vorne das kleinste Element steht. Im nächsten Durchgang betrachtet man den Index 2, durchsucht wiederum den Array nach dem kleinsten Element, wobei natürlich der Index 1 außen vor bleibt, und setzt das kleinste an den Index 2. Im 3. Durchgang bleiben dann die ersten beiden Elemente außen vor usw. So geht es immer weiter, bis man schließlich das vorletzte Element korrekt besetzt hat. Aus naheliegenden Gründen stimmt das letzte Element dann schon…

In Pascal sieht das Ganze so aus:

                         procedure SelSort(var Table: TableArray);
                         var
                            Elem     : LongInt;
                            Index    : LongInt;
                            Smallest : Byte;
                            SmallInd : LongInt;
 
                         begin
                            for Elem := 1 to TableSize - 1 do
                            begin
                               SmallInd := Elem;
                               Smallest := Table[SmallInd];
                               for Index := Elem + 1 to TableSize do
                               begin
                                  if Table[Index] < Smallest then
                                  begin
                                     Smallest := Table[Index];
                                     SmallInd := Index;
                                  end;
                               end;
                               if SmallInd <> Elem then
                               begin
                                  Table[SmallInd] := Table[Elem];
                                  Table[Elem] := Smallest;
                               end;
                            end;
                         end;

In der Variablen Smallest merkt sich der Algorithmus die Größe des bislang kleinsten Elementes, in SmallInd seine Position. Beide werden zunächst auf Elem initialisiert, d. h. auf die Position, die besetzt werden soll. Dann wird der übrige Array durchsucht, und wenn ein kleineres Element auftaucht, werden die beiden aktualisiert.

Zwei Besonderheiten sind beim Vertauschungsvorgang zu betrachten: Zum einen wird er nur ausgeführt, wenn tatsächlich eine neue Position gefunden wurde; zum anderen benötigen wir keinen Zwischenspeicher, weil der Wert des neuen Elementes ja noch in Smallest steht.

Selectionsort ist schneller als Bubblesort, - im Allgemeinen kann man vom Faktor 2 ausgehen - für größere Arrays jedoch auch nicht besonders gut geeignet.

Insertionsort steht für „Sortieren durch Einfügen“. Die Idee, die dem zugrunde liegt, ist einfach: Ein Teil am Anfang des Arrays, so wird angenommen, ist schon sortiert (zu Beginn ist dieser Teil natürlich 0 Elemente groß!). Nun wird das erste Element aus dem unsortierten Teil genommen und an der richtigen Stelle in den sortierten Teil eingefügt. Der sortierte Teil wächst dabei natürlich um ein Element, bleibt aber sortiert, wohingegen der unsortierte Teil um ein Element schrumpft.

Unser Algorithmus fängt also beim ersten Element an und geht dann bis zum letzten durch. Für jedes Element macht er nun folgendes: Von seiner Position aus bewegt er sich zum Anfang hin, solange die Elemente - wir sind ja im sortierten Teil - noch größer oder gleich dem in Frage stehenden Element sind. Dabei schiebt er jedes Element, das er überquert, eins nach hinten, so dass er immer eine Lücke vor sich herschiebt. Findet er dann einen kleineren Kandidaten, schiebt er die Lücke nicht weiter, sondern setzt sein Element hinein. Auf diese Weise verbindet der Algorithmus die Suche nach der richtigen Position mit dem Verschieben der darüberliegenden Elemente.

                         procedure InsSortLinear(var Table: TableArray);
                         var
                            Elem  : LongInt;
                            x     : Byte;
                            Index : LongInt;
                         begin
                            for Elem := 2 to TableSize do
                            begin
                               x := Table[Elem];
                               Index := Elem;
                               while (Index > 1) and (Table[Index - 1] >= x) do
                               begin
                                  Table[Index] := Table[Index - 1];
                                  Dec(Index);
                               end;
                               Table[Index] := x;
                            end;
                         end;

Wie man sieht, wird das Element zunächst in x gespeichert. Dann beginnt das Verschieben, bis entweder ein Element gefunden wird, das kleiner als x ist, oder bis man bei Index 1 angelangt ist. Im letzteren Fall hat man offenbar kein kleineres Element im sortierten Teil und plaziert das Element an Position 1. Um die richtige Position zu finden, verwendet diese Version von Insertionsort eine lineare Suche. Da liegt die Idee nicht fern, das Verfahren dadurch zu beschleunigen, dass man eine binäre Suche verwendet. Das Verschieben der „dahinterliegenden“ Elemente muss dann gesondert erledigt werden.

                         procedure InsSortBinary(var Table: TableArray);
                         var
                            Elem   : LongInt;
                            L, R   : LongInt;
                            Middle : LongInt;
                            Index  : LongInt;
                            x      : Byte;
                         begin
                            for Elem := 2 to TableSize do
                            begin
                               x := Table[Elem];
                               L := 1;
                               R := Elem;
                               while L < R do
                               begin
                                  Middle := (L + R) div 2;
                                  if Table[Middle] > x then R := Middle
                                  else if Table[Middle] < x then L := Middle + 1
                                  else R := L;
                               end;
                               for Index := Elem downto L + 1 do Table[Index] := Table[Index - 1];
                               Table[L] := x;
                            end;
                         end;

Auch in dieser verbesserten Version ist Insertionsort leider nicht unbedingt der Überflieger. Zwar ist es das schnellste der „langsamen“ Verfahren, bleibt aber hinter den schnelleren Algorithmen deutlich zurück.

Für die einen stellt Shellsort den idealen Kompromiss aus Einfachheit und Geschwindigkeit dar, für die anderen ist es uninteressant, weil schnellere Verfahren längst bekannt sind. Der einzige nach seinem Erfinder benannte Sortieralgorithmus hat jedenfalls nach wie vor eine große Anhängerschaft. Die Idee ist folgende: Der Array wird zunächst in mehrere Gruppen aufgeteilt, die dadurch festgelegt werden, daß zwischen ihren Mitgliedern der gleiche Abstand besteht. Angenommen, man verwendet den Abstand 3, dann gehören die Elemente 1, 4, 7, … in eine Gruppe, genauso 2, 5, 8, … und 3, 6, 9, … Diese Gruppen werden nun einzeln sortiert, dann wird der Abstand verringert und die Vorgehensweise wiederholt. Das macht man so lange, bis der Abstand 1 ist, so dass im letzten Schritt gar keine Unterteilung mehr stattfindet.

Es stellt sich die Frage, nach welcher Methode die Gruppen sortiert werden. Die Anwort ist Bubblesort nicht unähnlich, jedoch etwas schlecht zu erkennen. Für jeden Schritt gibt die Variable Gap den Abstand zwischen den Elementen an. Die Variable Index läuft alsdann von Gap + 1 bis zum hinteren Ende der Tabelle durch. Für jeden Wert von Index wird ein Sortierlauf gestartet, mit Index als oberer Grenze - welche Gruppe dabei sortiert wird, hängt also von Index ab. Die Variable j wird auf das nächstkleinere Element der Gruppe initialisiert (also Index - Gap), dann wird es mit dem nächsthöheren verglichen und ggf. vertauscht. Dann geht j wieder einen Schritt nach unten (Schrittweite Gap), usw., bis j < 0 ist.

Wenn Index das n. Element einer Gruppe zu fassen hat, sind also alle Elemente (dieser Gruppe) unterhalb dessen sortiert. Ist Index bis zum Ende durchgelaufen, sind alle Gruppen sortiert. Fragt sich nur noch, nach welchen Regeln der Abstand verringert werden soll. Im Beispiel unten wird er immer halbiert; es hat sich jedoch in Messungen ergeben, dass Shellsort schneller ist, wenn die Abstände immer ungerade sind (warum weiß der Himmel), wofür man ja sehr leicht sorgen kann. Die Schrittweiten wären dann z. B. 63, 31, 15, 7, 3, 1.

Einfacher zu verstehen als alle umständlichen Erklärungen ist wahrscheinlich der Pascal-Quelltext selbst:

                         procedure ShlSort(var Table: TableArray);
                         var
                            Gap   : LongInt;
                            x     : LongInt;
                            Index : LongInt;
                            j     : LongInt;
                         begin
                            Gap := TableSize div GapDivisor;
                            while Gap > 0 do
                            begin
                               for Index := Gap + 1 to TableSize do
                               begin
                                  j := Index - Gap;
                                  while j > 0 do
                                  begin
                                     if Table[j] <= Table[j + Gap] then
                                        j := 0
                                     else
                                     begin
                                        x := Table[j];
                                        Table[j] := Table[j + Gap];
                                        Table[j + Gap] := x;
                                     end;
                                     Dec(j,Gap);
                                  end;
                               end;
                               Gap := Gap div GapDivisor;
                            end;
                         end;

Shellsort legt eine bemerkenswerte Geschwindigkeit an den Tag, so dass man es schon fast zu den „schnellen“ Algorithmen zählen könnte. Leider kommt es mit sehr großen Arrays überhaupt nicht zurecht - heutzutage könnte man sagen, es skaliert schlecht (Vorsicht, Bastard Anglizismus from Hell!).

Wenn eine Methode schon Quicksort heißt, weckt das gewisse Ewartungen, und sie werden auch nicht enttäuscht: Quicksort ist in den meisten Fällen der schnellste Algorithmus. Was steckt dahinter?

Die Idee ist recht einfach: Man greift sich ein beliebiges Element des Arrays heraus - beispielsweise das mittlere - und teilt das Array in zwei Gruppen: Eine mit den Elementen, die größer sind als das herausgegriffene, und eine mit den kleineren (oder gleichen). Diese beiden Hälften übergibt man vertrauensvoll wiederum an Quicksort. Es handelt sich also um eine rekursive Funktion. Naja, und irgendwann sind die Arrays nur noch 1 Element groß und trivialerweise sortiert.

Um nun nicht immer neue Arrays erzeugen zu müssen, arbeitet Quicksort mit linker und rechter Grenze. Dafür müssen dann natürlich alle Elemente, die größer sind als das herausgegriffene, in den unteren Teil verschoben werden, die anderen in den oberen Teil. Darin besteht die eigentliche Arbeit von Quicksort:

                         procedure QSort(Links, Rechts : LongInt);
                         var
                            i, j : LongInt;
                            x, w : Byte;
                         begin
                            i := Links;
                            j := Rechts;
                            x := Table[(Links + Rechts) div 2];
                            repeat
                               while Table[i] < x do Inc(i);
                               while Table[j] > x do Dec(j);
                               if i <= j then
                               begin
                                  w := Table[i];
                                  Table[i] := Table[j];
                                  Table[j] := w;
                                  Inc(i);
                                  Dec(j);
                               end;
                            until i > j;
                            if Links < j then QSort(Links,j);
                            if Rechts > i then QSort(i,Rechts);
                         end;

In x wird zunächst das herausgegriffene Element gespeichert - in diesem Fall die Mitte. i und j sind Laufindizes, die zunächst links und rechts positioniert werden. Dann marschieren sie von beiden Seiten aufeinander zu, bis sie ein Element finden, das nicht auf ihre Seite gehört. Sollten sie sich zu diesem Zeitpunkt nicht schon überholt haben (in dem Fall würde es ja wieder stimmen), tauschen sie die beiden Elemente aus und machen weiter. Das wiederholt sich so lange, bis sich die beiden erreicht bzw. überholt haben. Anschließend wird QSort rekursiv aufgerufen, einmal für den unteren Teil, falls ein solcher überhaupt mit mehr als einem Element existiert, einmal für den oberen Teil (dito). Da die Rekursion nicht in der innersten Schleife stattfindet, ist sie relativ harmlos, allerdings kann das natürlich schon etwas auf den Stack gehen. Daher wird manchmal eine iterative Implementation empfohlen, bei der man den Stack selbst verwaltet; besonders trivial ist das leider nicht.

Quicksort ist, wie eingangs gesagt, in der Regel das schnellste Suchverfahren. Im schlimmsten Fall jedoch, wenn das herausgegriffene x jedesmal das größte (oder kleinste) Element des Arrays ist, fällt Quicksort leider auf das Niveau von Bubblesort herab. In den meisten Situationen fällt das nicht ins Gewicht, aber in Echtzeitanwendungen muss man es schon beachten.

Heapsort ist ebenfalls ein sehr schneller Algorithmus, aber im Durchschnitt nicht ganz so schnell wie Quicksort. Dafür leistet es sich auch im schlimmsten Fall keinen solchen Durchhänger wie dieses, so dass sich Heapsort vor allem für Anwendungen empfiehlt, in denen Höchstzeiten eingehalten werden müssen.

Die Funktionsweise ist leider nicht ganz trivial (finde ich). Man hat sich vorzustellen, dass die Elemente des Arrays tatsächlich in einem binären Baum gespeichert sind (näheres zu Bäumen findet sich übrigens auf www.bastisoft.de in der Rubrik über dynamische Datenstrukturen). Aber keine Angst, es kommt jetzt nicht die für binäre Bäume übliche Pointer-Orgie, denn es gibt einen Trick, mit dem man (ausgeglichene) binäre Bäume direkt im Array darstellen kann.

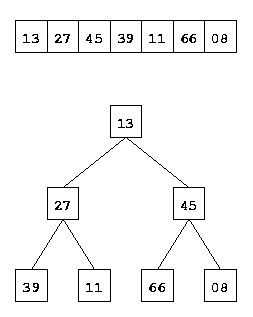
Dazu stellen wir uns erstmal vor, Element 1 des Arrays sei die Wurzel des Baums. Und weiter gilt: Jedes Element des Arrays, z. B. i, ist ein Knoten des Baumes, und seine beiden Nachfolger sind die Elemente 2 · i und 2 · i + 1. Die folgende Abbildung verdeutlicht, wie die Knoten im Array liegen:

Einen solchen Baum nennt man einen „Heap“ (engl. heap = Haufen), wenn jeder Knoten größer ist als seine Nachfolger. Die hintere Hälfte des Arrays - egal, in welchem Zustand er sich befindet - ist immer ein Heap, weil die Knoten ja gar keine Nachfolger mehr haben. Wenn der hintere Teil des Arrays (Hälfte oder mehr) ein Heap ist, kann ich diesen um ein Element nach vorne erweitern. Damit das Ergebnis immer noch ein Heap ist, muss ich das Element am neuen Knoten allerdings im Baum „absinken“ lassen (engl. to sift = sieben), wobei es immer mit dem größeren seiner Nachfolgeknoten vertauscht wird - so lange, bis beide Nachfolgeknoten kleiner sind.

Dieser Vorgang wird von der Prozedur Sift erledigt; wir werden ihn noch öfter brauchen:

                         procedure Sift(L, R : LongInt);
                         var
                            i, j : LongInt;
                            x    : Byte;
                         begin
                            i := L;
                            j := 2 * L;
                            x := Table[i];
                            if (j < R) and (Table[j + 1] > Table[j]) then Inc(j);
                            while (j <= R) and (Table[j] > x) do
                            begin
                               Table[i] := Table[j];
                               i := j;
                               j := j * 2;
                               if (j < R) and (Table[j + 1] > Table[j]) then Inc(j);
                            end;
                            Table[i] := x;
                         end;

Wie man sieht, bekommt Sift eine linke Grenze, dort fängt es an, und eine rechte Grenze, an der es aufhört - auch wenn das Array vielleicht noch weiterginge (es ist jetzt noch etwas unklar, wozu das gut sein soll: Geduld!). In x wird der Wert des zu „siftenden“ Elements gespeichert, i ist der aktuelle Knoten und j der Nachfolgeknoten - entweder 2 · i oder, wenn größer, 2 · i + 1.

Der erste Teil von Heapsort besteht genau darin, wie beschrieben von der Hälfte ausgehend den Heap nach vorne zu erweitern, bis das ganze Array ein Heap ist. Der zweite Teil, das eigentliche Sortieren, ist nun eigentlich auch nicht mehr schwer zu verstehen: Das erste Element des Arrays ist, weil es die Wurzel eines Heaps ist, das größte Element. Es gehört also ans Ende des Arrays. Setzen wir es doch einfach dorthin, indem wir es mit dem dortigen Element austauschen. Dieses ist nun an Position 1. Wir lassen es mit Hilfe von Sift einsinken - natürlich nur bis zum vorletzten Element, das letzte wollen wir in Ruhe lassen - und haben anschließend wieder das Maximum an Position 1 (weil die Knoten der zweiten Ebene ja auch die Maxima ihrer Unterheaps sind). Dieses vertauschen wir nun mit dem Element an vorletzter Stelle, lassen die neue Nummer 1 einsinken usw. usf. Wenn wir das ganzen Array besetzt haben, sind wir fertig, und weil das Array von unten her mit den jeweils größten Elementen aufgefüllt wurde, ist er sortiert - voilà!

Der Heapsort-Algorithmus in Pascal, die beiden Teile sind durch eine Leerzeile getrennt:

                         procedure HSort;
                         var
                            L, R  : LongInt;
                            Index : LongInt;
                            x     : Byte;
                         begin
                            L := (TableSize div 2) + 1;
                            R := TableSize;
                            while (L > 1) do
                            begin
                               Dec(L);
                               Sift(L,R);
                            end;
 
                            for Index := R downto 1 do
                            begin
                               x := Table[1];
                               Table[1] := Table[Index];
                               Table[Index] := x;
                               Sift(1,Index - 1);
                            end;
                         end;

Nun wird auch deutlich, warum Sift auch eine rechte Grenze mitbekommt. Eine mögliche Verbesserung besteht darin, dass man den Code von Sift gleich direkt in den Heapsort-Algorithmus schreibt. Dies sollte kein großes Problem sein, nur mit den Variablennamen muss man ein bisschen aufpassen. Ganz schön viel Aufwand für einen Sortieralgorithmus, könnte man sagen. Andererseits ist es halb so schlimm, wenn man es einmal verstanden hat. Und der Trick mit dem Unterbringen von binären Bäumen in Arrays ist ja auch etwas, das man sich merken kann.

Hörte es sich bis jetzt so an, als wären Quicksort und Heapsort die schnellsten Suchverfahren, so wirkt es vielleicht verwunderlich, aber das eher selten anzutreffende Bucketsort verspricht, noch schneller zu sein. Die Sache hat - natürlich - einen Haken: Bucketsort benötigt zusätzlichen Platz. Und zwar umso mehr, je größer die Menge der möglichen Schlüssel ist. Warum das so ist, wird gleich deutlich.

Das Prinzip ist einfach: In einem zusätzlichen Array namens Bucket gibt es für jeden möglichen Schlüssel ein „Fach“. Dann wird der Array Table von vorn bis hinten durchgegangen, und jedes Element wird in sein Fach gelegt. Anschließend braucht man nur noch den Inhalt der Fächer nacheinander zurück in das Array zu kopieren; dabei sollten die Fächer natürlich in der richtigen Reihenfolge sein. Anschließend ist das Array sortiert.

Leider ergibt sich eine Reihe von Problemen: Wie z. B. speichere ich mehrere Elemente in einem Feld des Bucket-Arrays? Diese Elemente müssen ja nicht unbedingt gleich sein, sie haben nur den gleichen Sortierschlüssel! Hierfür gibt es verschiedene Lösungen, aber die naheliegendste ist, eine linked List zu verwenden.

Zum anderen möchte man häufig Strings sortieren, aber selbst von Strings der Länge 10 gibt es 2610 = 1.411671 · 1014 Möglichkeiten. Von Standard-Strings der Länge 255 will ich mal lieber gar nicht anfangen… Auch das Sortieren von LongInts mit ihren 32 Bit Länge dürfte wenig spaßig sein. Ein Ausweg besteht darin, den Schlüssel in seine Einzelelemente aufzuteilen und mehrmals zu sortieren; bei Strings wird also zuerst nach dem letzten Zeichen sortiert, dann nach dem vorletzten usw. Bei Zahlen kann man entsprechend nach einzelnen Bits sortieren.

Um den Algorithmus zu verdeutlichen, will ich aber ein viel simpleres Beispiel nehmen: Es werden Bytes sortiert, der Bereich, innerhalb dessen sie Werte annehmen dürfen, ist also 0 bis 255. Eine starke Vereinfachung besteht darin, daß die Zahlen nur aus dem Schlüssel bestehen können, und zwei Elemente mit dem gleichen Schlüssel nicht unterscheidbar sind. Daher brauchen sie nicht in den Fächern gespeichert zu werden - der Index des Faches ist schon der Wert, und im Fach wird einfach gezählt, wie oft die betreffende Zahl schon aufgetreten ist. So oft wird sie dann beim Zurückschreiben in das Array wiederholt.

Und so sieht die Prozedur aus:

                         procedure BuckSort;
                         var
                            Index     : LongInt;
                            BuckIndex : LongInt;
                         begin
                            for BuckIndex := 0 to 255 do Bucket[BuckIndex] := 0;
                            for Index := 1 to TableSize do
 
                               Inc(Bucket[Table[Index]]);
                            Index := 1;
                            BuckIndex := 0;
                            while Index <= TableSize do
                            begin
                               while Bucket[BuckIndex] = 0 do
                                  Inc(BuckIndex);
                               Table[Index] := BuckIndex;
                               Dec(Bucket[BuckIndex]);
                               Inc(Index);
                            end;
                         end;

In dieser Version ist Bucketsort ziemlich schnell. Eine andere Anwendung, in der es glänzt, ist z. B. das Sortieren von Strings nach Anfangsbuchstaben. Insgesamt jedoch fordert der Geschwindigkeitsvorteil seinen Tribut in Form von allerlei Umständlichkeiten, die einem mit Quicksort und Heapsort erspart bleiben. Das ist auch der Grund dafür, daß Bucketsort zumeist nur in Spezialfällen angewendet wird