Inhaltsverzeichnis
Das Binärsystem
Computer können lediglich mit zwei Zuständen arbeiten. Im Allgemeinen bezeichnet man diese Zustände mit 0 und 1. Die Speichereinheit, die genau das speichern kann, nennt man Bit. Das hat zur Folge, dass Zahlen aus unserem System (Dezimalsystem) in das des Computers (Binärsystem) und umgekehrt umgerechnet werden müssen. Die notwendigen Verfahren dazu werden in diesem Kapitel vorgestellt. Physikalisch werden die Zustände 0 und 1 mit 'Spannung liegt an' und 'Spannung liegt nicht an' realisiert.
Hinweise:
- Nicht immer ist es so einfach, das 0 'Spannung liegt nicht an' bedeutet. Auf CDs wird beispielsweise dafür gesorgt, dass 'Loch' und 'Nicht-Loch' möglichst gleichverteilt bleiben - unabhängig von den Daten.
- Stelle := Die Zahl 7473 hat 4 Stellen.
- Ziffer := Das Dezimalsystem hat 10 Ziffern.
- In Binärzahlen werden meist zur besseren Lesbarkeit je 4 Ziffern gruppiert und dazwischen Leerzeichen eingefügt. Bsp.: 0100 0111 1000 0101
Stellenwertsystem im Binärsystem
Wie man das aus dem Dezimalsystem kennt, hat auch im Binärsystem eine Ziffer einen anderen Wert, wenn sie an einer anderen Position in einer Zahl steht. Beispiel aus dem Dezimalsystem: 7374 - Hier hat die 7 einmal den Stellenwert 7000 und einmal 70. Dieser Wert resultiert daraus, dass wir 10 Ziffern zur Verfügung haben. Daher auch der Name 'Dezimal'system. Man kann den Stellenwert berechnen, indem die Ziffer mit einer Potenz multipliziert wird. Am einfachsten wird das wieder an einem Beispiel deutlich:
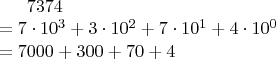
Im Binärsystem verläuft das analog. Lediglich die Zahl der Ziffern ist eine andere, wodurch sich auch die Potenzen ändern. Beispiel:
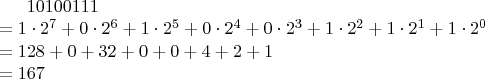
Man beachte, dass die letzten drei Zeilen im Dezimalsystem notiert sind. Da hier aus einer Binärzahl eine Dezimalzahl gemacht wurde, ist dies ein Verfahren, mit dem man Binärzahlen in Dezimalzahlen umrechnen kann.
Umrechnen vom Dezimalsystem ins Binärsystem
Zwei mögliche Verfahren:
Mit Tabelle
Weiß man die 2er-Potenzen auswendig und ist einigermaßen fit im Kopfrechnen (meist wird an dieser Stelle schon das andere Verfahren gewählt), so kann man folgende Tabelle verwenden:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|
Anschließend wird in jeder Spalte eine 1 eingetragen, die zur Summe der gesuchten Zahl beitragen kann. In den anderen Spalten wird eine Null eingetragen. Beispiel: 177
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
Um herauszufinden, welche Zahlen das sind, beginnt man links. Ist die größte Zahl (hier die 128) kleiner als die umzuwandelnde Zahl (hier 177), so wird dort eine 1 eingetragen und die jeweilige Zahl von der gesuchten abgezogen (177-128=49). Mit dieser Differenz wird nun genauso weiterverfahren. Die größte 2er-Potenz, die kleiner als 49 ist, ist 32. Also kommt in die betreffende Spalte eine 1 und 32 wird von 49 subtrahiert. Usw….
Ohne Tabelle
Auch hier wird das Verfahren am Einfachsten durch ein Beispiel erläutert:
177 : 2 = 88 Rest 1 88 : 2 = 44 Rest 0 44 : 2 = 22 Rest 0 22 : 2 = 11 Rest 0 11 : 2 = 5 Rest 1 5 : 2 = 2 Rest 1 2 : 2 = 1 Rest 0 1 : 2 = 0 Rest 1
Anschließend werden die Reste sämtlicher Divisionen in umgekehrter Reihenfolge aufgeschrieben und ergeben so die gesuchte Binärdarstellung.
Das Verfahren endet erst, wenn bei einer Division 0 herauskommt. Der Rest spielt bei der Entscheidung, ob weitergerechnet werden muss oder nicht, keine Rolle.
Umrechnen vom Binärsystem ins Dezimalsystem
Das Verfahren dazu wurde schon beim Erläutern der Stellenwerte eingeführt.
Übungsaufgaben: Rechne folgende Zahlen ins Dezimalsystem um:
- 1010 1010
- 1111 0000
- 1000 0000 0000 0001
(Nach je vier Ziffern wurde ein Leerzeichen lediglich für bessere Lesbarkeit eingefügt.)
Ganze Zahlen im Binärsystem ohne Vorzeichen
Natürlich könnte man im Binärsystem auch Vorzeichen wie + und - definieren. Da diese technisch aber nicht realisierbar sind, muss wieder nur mit 0 und 1 gearbeitet werden. Das größte Bit (ganz links) wird dafür als Vorzeichen genutzt. Eine 1 kennzeichnet hier eine negative Zahl und die 0 entsprechend eine nicht negative Zahl. Dies hat zur Folge, dass immer mit einer konstantent Bandbreite (Ziffern der Binärzahl) gearbeitet werden muss, da sonst nicht klar ist, welches das größte Bit ist.
Wie wird eine negative Zahl nun im Binärsystem dargestellt? Dies folgt aus der Überlegung, dass die Rechung 4 + (-2) korrekterweise 2 ergeben muss. Bei einer Bandbreite von 4 Bit ergibt sich daher:
0100 + ???? ------ 0010
Durch die binäre Addition muss für die (-2)
1110
stehen, damit das richtige Ergebnis herauskommt. Man beachte, dass bei der Addition ein Übertrag herauskommt, der anschließend weggelassen wird. Führt man diese Überlegung mit sämtlichen weiteren (möglichen) Zahlen durch, so kommt man zu folgender Zuordnung zwischen ganzen Zahlen:
0000 ±0 0001 +1 0010 +2 0011 +3 0100 +4 0101 +5 0110 +6 0111 +7 1000 -8 1001 -7 1010 -6 1011 -5 1100 -4 1101 -3 1110 -2 1111 -1
Bei 1 Byte (8 Bit) Bandbreite ergeben sich demnach Zahlen von 0 bis 127 und von -128 bis -1. Da auch hier die Formel für die Zahl der Möglichkeiten: 2^n gilt. Wobei n die Bandbreite angibt.
Negative Dezimalzahlen ins Binärsystem und umgekehrt umwandeln
- Wandle die Dezimalzahl ohne Beachtung des Vorzeichens in eine Binärzahl um.
- Invertiere alle Bits. (Tausche Einsen gegen Nullen aus und umgekehrt.) - Das Ergebnis nennt man Einerkomplement.
- Addiere 1. Das Ergebnis nennt man Zweierkomplement.
Beachte: Es muss immer angegeben werden, ob negative Zahlen möglich sein sollen, da sonst nicht klar ist, welche Bedeutung Binärzahlen haben, die mit einer 1 beginnen.
Beispiele
- Bandbreite 4 Bit, Umrechnung von -5
5 = 0101
Einerkomplement: 1010
Zweierkomplement: 1011
⇒ -5 = 1011 - Bandbreite 8 Bit, Umrechnung von -5
5 = 0000 0101
Einerkomplement: 0000 1010
Zweierkomplement: 1111 1011
⇒ -5 = 1111 1011
Hier wird deutlich, dass eine feste Bandbreite umumgänglich ist, wenn negative Zahlen dargestellt werden können sollen. - Bandbreite 8 Bit, Umrechung von -116
116 = 01110100
Einerkomplement: 10001011
Zweierkomplemet: 10001100
⇒ -116 = 10001100
Aufgaben
- Rechne die Zahl -104 bei einer Bandbreite von 16 Bit ins Binärsystem um.
- Rechne die Zahl -94 bei einer Bandbreite von 8 Bit ins Binärsystem um.
- Warum kann man die Zahl -134 bei einer Bandbreite von 8 Bit nicht im Binärsystem darstellen?
- Negative Zahlen sollen möglich sein. Wie lautet die Dezimalzahl, die durch lauter Einsen dargestellt wird? Warum spielt die Bandbreite hier keine Rolle?