Inhaltsverzeichnis
Informatik-Buch - Informationsverarbeitung
Das Hexadezimalsystem
Das hexadezimale Zahlensystem stellt Zahlen mit Hilfe von 16 Ziffern dar:
0 1 2 3 4 5 6 7 8 9 0 A B C D E F
Dementsprechend kann man mit 2 Ziffern die Zahlen von 0 bis 255 (=162-1) darstellen. So wird gezählt:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10,11,12,13,14,15,16,17,18,19,1A,1B,1C,1D,1E,1F, 20,21,22,23,24,25,26,27,28,29,2A,2B,2C,2D,2E,2F, 30,31,32,33,34,35,36,37,38,39,3A,3B,3C,3D,3E,3F, 40,41,42,43,44,45,46,47,48,49,4A,4B,4C,4D,4E,4F, 50,51,52,53,54,55,56,57,58,59,5A,5B,5C,5D,5E,5F, 60,61,62,63,64,65,66,67,68,69,6A,6B,6C,6D,6E,6F, 70,71,72,73,74,75,76,77,78,79,7A,7B,7C,7D,7E,7F, 80,81,82,83,84,85,86,87,88,89,8A,8B,8C,8D,8E,8F, 90,91,92,93,94,95,96,97,98,99,9A,9B,9C,9D,9E,9F, A0,A1,A2,A3,A4,A5,A6,A7,A8,A9,AA,AB,AC,AD,AE,AF, B0,B1,B2,B3,B4,B5,B6,B7,B8,B9,BA,BB,BC,BD,BE,BF, C0,C1,C2,C3,C4,C5,C6,C7,C8,C9,CA,CB,CC,CD,CE,CF, D0,D1,D2,D3,D4,D5,D6,D7,D8,D9,DA,DB,DC,DD,DE,DF, E0,E1,E2,E3,E4,E5,E6,E7,E8,E9,EA,EB,EC,ED,EE,EF, F0,F1,F2,F3,F4,F5,F6,F7,F8,F9,FA,FB,FC,FD,FE,FF.
Wobei die einziffrigen Zahlen meist auch 2-ziffrig dargestellt werden:
00,01,02,03,04,05,06,07,08,09,0A,0B,0C,0D,0E,0F.
Dies hat insgesamt den Vorteil, dass sämtliche Zahlen, die mit Hilfe eines Bytes codiert werden können, mit Hilfe von genau 2 hexadezimalen Ziffern dargestellt werden können. Und umgekehrt: Mit 2 hexadezimalen Ziffern lassen sich genau soviele Zahlen darstellen, wie mit Hilfe eines Bytes codiert werden kann.
Stellenwertsystem im Hexadezimalsystem
Wie man das aus dem Dezimalsystem kennt, hat auch im Hexadezimalsystem eine Ziffer einen anderen Wert, wenn sie an einer anderen Position in einer Zahl steht. Beispiel aus dem Dezimalsystem: siehe 1)
Im Hexadezimalsystem verläuft das analog. Lediglich die Zahl der Ziffern ist eine andere, wodurch sich auch die Potenzen ändern. Beispiel:
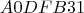
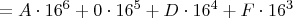
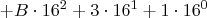
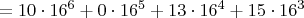
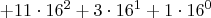
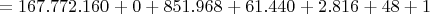
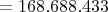
Man beachte, dass die letzten drei Zeilen im Dezimalsystem notiert sind, während die zweite Zeile eine Mischung aus beiden System ist. Da hier aus einer Hexadezimalzahl eine Dezimalzahl gemacht wurde, ist dies ein Verfahren, mit dem man Hexadezimalzahlen in Dezimalzahlen umrechnen kann.
Umrechnen vom Dezimalsystem ins Hexadezimalsystem
Zwei mögliche Verfahren:
Mit Tabelle
Weiß man die 16er-Potenzen auswendig und ist einigermaßen fit im Kopfrechnen… Ja, ja. So fing das im Binärsystem an. Hier sind es allerdings 16er-Potenzen, die erheblich unhandlicher sind. Wem es Spaß macht, den will ich nicht daran hindern, auch hier die Tabelle zu benutzen. Empfehlen kann ich das allerdings nicht…
Die Zahl
| 115.828.048.539 |
|---|
ergibt, wie man leicht sieht:
| 68.719.476.736 | 4.294.967.296 | 268.435.456 | 16.777.216 | 1.048.576 | 65.536 | 4.096 | 256 | 16 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | A | F | 7 | E | 3 | C | 2 | 9 | B |
Ohne Tabelle
Auch hier wird das Verfahren am Einfachsten durch ein Beispiel erläutert:
57019 : 16 = 3563 Rest 11 3563 : 16 = 222 Rest 11 222 : 16 = 13 Rest 14 13 : 16 = 0 Rest 13 => 13 14 11 11 = DEBB
Anschließend werden auch hier die Reste sämtlicher Divisionen in umgekehrter Reihenfolge aufgeschrieben und ergeben so die gesuchte Hexadezimaldarstellung. Das Verfahren wiederum endet erst, wenn bei einer Division 0 herauskommt. Der Rest spielt bei der Entscheidung, ob weitergerechnet werden muss oder nicht, keine Rolle!
Umrechnen vom Hexadezimalsystem ins Binärsystem
Da eine hexadezimale Ziffer genau 16 verschiedene Zustände beschreiben kann und das ebenso für 4 binäre Ziffern gilt, kann zwischen diesen beiden Systemen besonders einfach umgerechnet werden. Beispiel:
ABF4CD98 = 1010 1011 1111 0100 1100 1101 1001 1000
da
A = 1010 B = 1011 F = 1111 4 = 0100 C = 1100 D = 1101 9 = 1001 8 = 1000
Es kann also jede hexadezimale Ziffer einzeln betrachtet werden. Umgekehrt müssen immer 4 Bit zusammengefasst werden.
Übungsaufgaben: Rechne folgende Zahlen ins Hexadezimalsystem um:
- 1010 1010
- 1111 0000
- 1000 0000 0000 0001
(Nach je vier Ziffern wurde, wie üblich, ein Leerzeichen lediglich für bessere Lesbarkeit eingefügt.)
Aufgaben
(billiger Tipp: Notiere zunächst die 16er Reihe… - Nein, nicht nur bis 10*16, sondern bis 16*16!)
- Rechne die Zahl 136704 ins Hexadezimalsystem um. Benutze keinen Taschenrechner.